1. PENGERTIAN VEKTOR
Pada garis berarah dari titik A ke titik B di R 3 mempunyai panjang tertentu dinyatakan sebagai vektor. Vektor dapat dinotasikan dengan :
Atau dapat juga dinyatakan sebagai :

Dimana
 adalah vektor satuan.
adalah vektor satuan.
2. Panjang Vektor
Jika titik A (x1,y1,z1) dan B (x2,y2,z2) maka vektor AB adalah :



3. Vektor Satuan
Vektor satuan adalah adalah vektor yang panjangnya satu satuan. Jika vektor
maka vektor satuan dari a adalah:

4. Operasi
Penjumlahan, Pengurangan dan Perkalian Vektor dangan Skalar a. Penjumlahan atau pengurangan vektor
Contoh :
Diketahui vektor
 Nilai
Nilai  Jawab :
Jawab :


b. Perkalian Skalar dengan vektor

5. Rumus Perbandingan, Perkalian Skalar Proyeksi dan Perkalian Silang Vektor
a. Perkalian Skalar
b. Cross Product




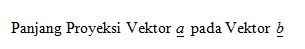
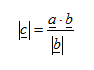
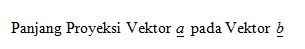

d. Rumus Pembagian


Contoh : Diketahui titik A (-4, 1, 3 ), B (6, -4, 3) dan C (4, 5, -1) Titik R membagi AB sehingga 2AR = 3RB, vektor yang mewakili
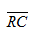 adalah :
adalah :
Jawab :


RUMUS TRANSRORMASI
TRANSFORMASI GEOMETRI
Jenis-jenis transformasi yang dapat dilakukan antara lain :
- Translasi (Pergeseran)
- Refleksi (Pencerminan)
- Rotasi (Perputaran)
- Dilatasi (Perkalian)
2. Translasi dan Operasinya
Translasi (pergeseran) adalah pemindahan suatu objek sepanjang garis lurus dengan arah dan jarak tertentu.
Jika translasi
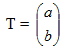 memetakan titik P (x, y) ke titik P’(x’, y’) maka x’ = x + a dan y’ = y + b atay P’ (x + a, y + b ) ditulis dalam bentuk :
memetakan titik P (x, y) ke titik P’(x’, y’) maka x’ = x + a dan y’ = y + b atay P’ (x + a, y + b ) ditulis dalam bentuk : 
Contoh : Tentukan koordinat bayangan titik A (-3, 4) oleh translasi

Jawab :
Jawab :
A’ = ( -3 + 3, 4 + 6)
A’ = (0, 10)
3. Refleksi (Pencerminan)
a. Pencerminan terhadap sumbu x
Matriks percerminan :
b. Pencerminan Terhadap sumbu y
Matriks Pencerminan:
c. Pencerminan terhadap garis y = x
d. Pencerminan terhadap garis y = -x
Matriks Pencerminan:
e. Pencerminan terhadap garis x = h
Sehingga:
f. Pencerminan terhadap garis y=k
Sehingga:
g. Pencerminan terhadap titik asal O (0, 0)
Sehingga:
h. Pencerminan terhadap garis y = mx dimana m = tan q
Contoh :
Jawab :
Ambil sembarang titik pada garis y = 2x – 5, misalnya (x, y) dan titik bayangan oleh translasi  adalah (x’, y’) sehingga ditulis
adalah (x’, y’) sehingga ditulis 
 adalah (x’, y’) sehingga ditulis
adalah (x’, y’) sehingga ditulis 
Atau
Persamaan (1) dan (2) disubtitusikan pada persamaan garis semula, sehingga :
y = 2x – 5
y’ + 2 = 2 (x’- 3) – 5
y’ = 2x’ – 6 – 5 – 2
y’ = 2x’ – 13
Jadi persamaan garis bayangan y = 2x – 5 oleh translasi  adalah y = 2x – 13 .
adalah y = 2x – 13 .Sumber:
http://mainmatematika.blogspot.co.id/2012/04/vektor.html







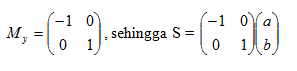


















Berikan Komentar:
0 comments: