PERTIDAKSAMAAN

CONTOH PERTIDAKSAMAAN
Sumber Foto: https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhzHWcQEEFtNvTDXGBxudNudFwcRMguUlTL6ud6rhmSANAoLCJGvhrkAlS0peeYATYtCSjm2y-hxGhu099Fs-78GPPVHtQpWgyt0VVdHX6zY0Hgto8NVB-OZMubcXT5k5Ht1dZBTSqoUyQ/s1600/Mat.X.IPA.Peminatan+-+Pert.Pecahan.png

Pengertian Pertidaksamaan

Pertidaksamaan adalah kalimat terbuka yang menyatakan hubungan dua hal tidak mempunyai kesamaan atau tidak sama dengan. Hubungan tidak sama dengan dapat dinotasikan dengan tanda:

< (kurang dari)

≤ (kurang dari atau sama dengan)

> (lebih dari)
≥ (lebih dari atau sama dengan)

Jika ada pertidaksamaan x < a maka niai x yang memenuhi adalah lebih kecil dari a dan dalam garis bilangan dilukiskan seperti

Jika ada pertidaksamaan matemati x ≥ a maka nilai x yang memenuhi adalah lebih besar dari a dan dalam garis bilangan dilukiskan

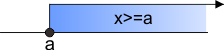
Sifat-sifat Pertidaksamaan Matematika

Sobat hitung menjadi sangat penting untuk mengetahui sifat pertidaksamaan sebagai hal mendasar untuk mengerjakan berbagai macam soal. Berikut sifat-sifat dari pertidaksamaan matematika. 

1. Tanda pertidaksamaan tidak akan berubah jika sobat menambahkan atau  mengurangkan suatu pertidaksamaan dengan bilangan atau suatu ekspresi matematika tertentu

Jika a > b maka:
a+c > b+c ; a-c > b-c
Jika a<b maka:
a+c < b+c ; a-c < b-c
misalnya
x + 6 > 8 ⇒ x+6-6 > 8-6 ⇒ x > 2

2. Tanda pertidaksamaan tidak akan berubah jika sobat mengalikan atau membaginya dengan bilangan POSITIF

Jika a > b dan c > 0 maka
ac > bc dan a/c > b/c
milsalkan
4x ≥ 12, Jika sobat membagi masing masing ruas dengan angka 4 (positif) 4x/4 ≥ 12/ 4 ⇒ x  ≥ 3

3. Tanda pertidaksamaan akan berbalik jika dikali atau dibagi dengan sebuah bilangan NEGATIF

Jika a > b dan c < 0 maka:
ac < bc dan a/c < b/c (amati bahwa tanda berbalik)
Banyak sobat hitung yang mungkin lupa dengan keharusan membalik tanda. Contohnya seperti berikut

-3x ≥ 9 untuk menyelesaikan pertidaksamaan tersebut sobat harus membagi tiap ruas kanan dan kiri dengan -3 atau dengan kata lain mengalikan tiap ruas dengan -1/3. Karena dikali dengan bilangan negatif maka tanda wajib berbalik.
-3x ≥ 9 ⇒ -3x/-3 ≤ 9/-3 ⇒ x ≤ -3 (amati tanda berbalik)

4. Eksponen (Pemangkatan) Pertidaksamaan

Ada yang unik dari pemangkatan pertidaksamaan matematika, tanda pertidaksamaan berbalik tergantung dari ganjil atau genapanya pangkatnya.

jika  a > b > 0 maka
a² > b² > 0
a³ > b³ > 0
a⁴ > b⁴ > 0
a⁵ > b⁵ > 0
dan seterusnya. Secara umum an > bn ; a bilangan asli

jia a < b < 0 maka
a² > b² > 0
a³ < b³ < 0
a⁴ > b⁴ > 0
a⁵ < b⁵ < 0
dan seterusnya. Secara umum aⁿ > bⁿ, jika n genap dan aⁿ < bⁿ jika n ganjil.

Contoh
x < -2 jika sobat pangkatkan dua didapat x² > (-2)² (tanda berubah jika n genap akan selalu aⁿ > bⁿ) dan logikanya masuk jika x saja kurang dari -2 (-3, -4, -5, dst) pasti x² hasilnya akan selalu lebih dari 4, -3² = 9; -4² = 16, dst.

Bentuk-Bentuk Pertidaksamaan Kuadrat

Selama ini ada beberapa bentuk pertidaksamaan kuadrat, diantaranya:

Pertidaksamaan Linier

Pertidaksamaan dengan vaiable berpangkat 1
Contoh
Tentukan nilai x yang memenuhi pertidaksamaan 3x-2 < x+8
Jawab
3x-2 < x+8
3x-x < 8+2
2x < 10
x<5

Pertidaksamaan Kuadrat

Cobat sobat tentukan nilai x dari pertidaksamaan kuadrat berikut x²-x-6≤0
Jawab:
x²-x-6 ≤ 0
(x-3) (x+2) ≤ 0
x₁ = 3 dan x₂ = -2
garis bilangan dari pertidaksamaan (x-3) (x+2) ≤ 0

dari gambar di atas sobat sudah tahu mana area yang menghasilkan nilai positif dan negatif. Kemudian karena tanda pertidaksamaan adalah  ≤ 0 maka nilai yang memenuhi pertidaksamaan matematika (x-3) (x+2) ≤ 0 adalah yang menghasilkan x²-x-6 ≤ 0 bernilai negatif yaitu -2≤x≤3

Pertidaksamaan Polinom

contoh
x³ – 2x² – 15x < 0
x (x² – 2x – 15) < 0
x (x-5) (x+3) < 0
x₁ = 0 ; x₂ = 5 ; x₃ = -3

nilai x kemudian kita letakkan pada garis bilangan

Karena tanda pertidaksamaan < maka nilai yang memenuhi adalah nilai x yang menghasilkan x³ – 2x² – 15x < 0 bernilai negatif (-) yaitu x < -3 dan 0 < x < 5.

Pertidaksamaan Harga Mutlak

Nilai mutlak dinyatakan dengan tanda kurung pagar. Mutlak dari x dinyatakan dengan notasi ∣x∣. Yang dimaksud dengan nilai atau harga mutlak dari suatu bilangan sama dengan nilaipositif dari bilangan tersebut. Misal nih

∣3∣= 3 dan ∣3∣ = 3

jadi dalam nilai/ harga mutlak berlaku x untuk  x ≥ 0 dan -x untuk x < 0.

Pertidaksamaan harga mutlak merupakan pertidaksamaan yang variabelnya berada di dalam tanda mutlak. Sifat-sifat dari harga mutlak sebagai berikut

Untuk a > 0 maka
∣x∣< a jika dana hanya jika -a < x < a
∣x∣> a jika dan hanya jika x<-a atau x > a

Contoh
tentukan nilai x yang memenuhi pertidaksamaan
∣2x-1∣ < 5

⇒    -5 < 2x-1 < 5
-5+1 < 2x-1+1 <5+1 (masing-masing ruas ditambah 1)
-4 < 2x < 6 (masing-masing ruas dibagi 2)
-2 < x < 3
jadi nilai x yang memenuhi pertidaksamaan adalah -2 < x < 3

Contoh Berikutnya
∣2x-1∣ ≥ 3
⇒ 2x-1 ≤ -3 atau  2x-1 ≥ 3
2x-1 ≤ -3
2x ≤ -2
x ≤ -1
2x-1 ≥ 3
2x ≥ 4
x ≥ 2

Sumber:

http://rumushitung.com/2013/08/24/pertidaksamaan-matematika-sma/